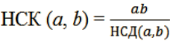приклад
Найменше
спільне
кратне
спільне
кратне

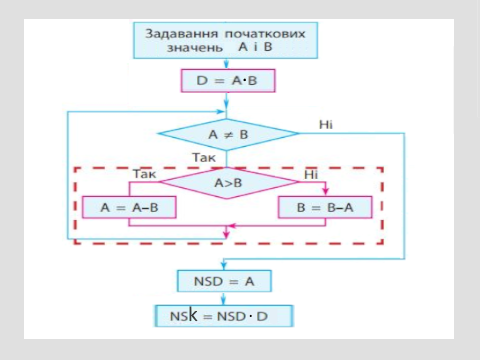
Найменше спільне кратне (НСК) — найменше натуральне число, яке ділиться на кожне з даних чисел.
Наприклад, НСК(6,4)=12.
Щоб знайти НСК двох чисел, необхідно:
1) розкласти дані числа на прості множники;
2) скласти добуток усіх простих множників;
3) обчислити складений добуток.
Приклад. Знайдемо найменше спільне кратне чисел 8 і 14
Розкладаємо числа на прості множники:
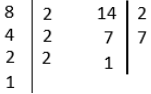
8 = 2 • 2 • 2
14 = 2 • 7
Допишемо добуток множників з другого розкладання, яких нема в першому (оскільки 2 вже є, виписуємо лише множник 7)
Перемножимо ці прості множники і отримаємо:
2 • 2 • 2 • 7 = 56 - найбільший спільний дільник
Відповідь: НСК (8; 14) = 56
* Найменше спільне кратне двох чисел дорівнює добутку цих чисел, поділеному на їх найбільший спільний дільник.
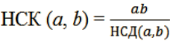
Наприклад, НСК(6,4)=12.
Щоб знайти НСК двох чисел, необхідно:
1) розкласти дані числа на прості множники;
2) скласти добуток усіх простих множників;
3) обчислити складений добуток.
Приклад. Знайдемо найменше спільне кратне чисел 8 і 14
Розкладаємо числа на прості множники:
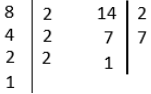
8 = 2 • 2 • 2
14 = 2 • 7
Допишемо добуток множників з другого розкладання, яких нема в першому (оскільки 2 вже є, виписуємо лише множник 7)
Перемножимо ці прості множники і отримаємо:
2 • 2 • 2 • 7 = 56 - найбільший спільний дільник
Відповідь: НСК (8; 14) = 56
* Найменше спільне кратне двох чисел дорівнює добутку цих чисел, поділеному на їх найбільший спільний дільник.