приклад
Найбільший
спільний
дільник
спільний
дільник

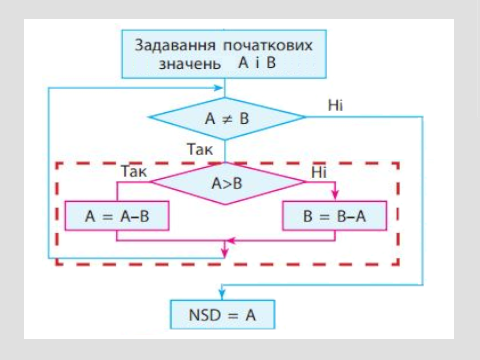
Найбільший спільний дільник (НСД) — найбільше натуральне число, на яке без остачі ділиться кожне з даних чисел.
Наприклад, НСД(16,28)=4.
Щоб знайти НСД двох або кількох чисел, необхідно:
1) розкласти дані числа на прості множники;
2) скласти добуток усіх спільних простих множників;
3) обчислити складений добуток.
Приклад 1. Знайдемо найбільший спільний дільник чисел 48 і 60
Розкладаємо числа на прості множники:
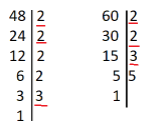
48 = 2 • 2 • 2 • 2 • 3
60 = 2 • 2 • 3 • 5
Знаходимо добуток спільних множників:
2 • 2 • 3 = 12 - найбільший спільний дільник
Відповідь: НСД (48; 60) = 12
Aлгоритм Евкліда
Для знаходження НСД двох даних чисел використовують чудовий процес, який ґрунтується на послідовному діленні.
Щоб знайти НСД двох даних чисел за допомогою алгоритму Евкліда, треба більше число поділити на менше (зменшуємо більше!).
Якщо ділення виконалось без остачі, то НСД є менше число.
Якщо при діленні вийшла остача, то менше число треба поділити на цю остачу; потім першу остачу поділити на другу і т.д., до тих пір, поки ділення не виконається без остачі.
Перший дільник, при якому ділення виконається без остачі, й буде НСД двох даних чисел.
Приклад 2. Знайдемо НСД чисел 112 і 80.

При діленні 112 на 80 дістаємо в остачі 32.
При діленні 80 на 32 дістаємо в остачі 16.
Ділення 32 на 16 виконалось без остачі.
Отже, НСД чисел 112 і 80 дорівнює 16
Відповідь: НСД (112, 80) = 16
Якщо найбільший спільний дільник заданих чисел дорівнює 1, то такі числа називають взаємно простими.
Наприклад, НСД(16,28)=4.
Щоб знайти НСД двох або кількох чисел, необхідно:
1) розкласти дані числа на прості множники;
2) скласти добуток усіх спільних простих множників;
3) обчислити складений добуток.
Приклад 1. Знайдемо найбільший спільний дільник чисел 48 і 60
Розкладаємо числа на прості множники:

48 = 2 • 2 • 2 • 2 • 3
60 = 2 • 2 • 3 • 5
Знаходимо добуток спільних множників:
2 • 2 • 3 = 12 - найбільший спільний дільник
Відповідь: НСД (48; 60) = 12
Aлгоритм Евкліда
Для знаходження НСД двох даних чисел використовують чудовий процес, який ґрунтується на послідовному діленні.
Щоб знайти НСД двох даних чисел за допомогою алгоритму Евкліда, треба більше число поділити на менше (зменшуємо більше!).
Якщо ділення виконалось без остачі, то НСД є менше число.
Якщо при діленні вийшла остача, то менше число треба поділити на цю остачу; потім першу остачу поділити на другу і т.д., до тих пір, поки ділення не виконається без остачі.
Перший дільник, при якому ділення виконається без остачі, й буде НСД двох даних чисел.
Приклад 2. Знайдемо НСД чисел 112 і 80.

При діленні 112 на 80 дістаємо в остачі 32.
При діленні 80 на 32 дістаємо в остачі 16.
Ділення 32 на 16 виконалось без остачі.
Отже, НСД чисел 112 і 80 дорівнює 16
Відповідь: НСД (112, 80) = 16
Якщо найбільший спільний дільник заданих чисел дорівнює 1, то такі числа називають взаємно простими.

