приклад
Метод порівняння


Спосіб порівняння часто використувужться, якщо при змінних однакові коефіцієнти.
Переглянемо всі рівняння системи і виберемо змінну, щоб вона мала однакові коефіцієнти в цих рівняннях системи.
Виражаємо вибрану змінну в обох рівняннях. Отримані рівняння прирівнюємо та обчислюємо їх змінну.
Підставляємо цю змінну в одно з рівнянь системи. Обчислюємо другу змінну.
Приклад: Розвяжіть рівняння:
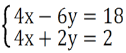
Розв'зування:
Виражаємо відносно 4x:
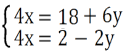
Прирівнюємо отримані рівняння та знаходимо значення
змінної y:
18 + 6y = 2 - 2y;
8y = -16;
y = -2
Підставляємо y і знаходимо значення x з другого рівняння системи:
4x = 2 - 2*(-2);
4x = 6 ;
x = 1,5
Відповідь: (1,5;4)
Переглянемо всі рівняння системи і виберемо змінну, щоб вона мала однакові коефіцієнти в цих рівняннях системи.
Виражаємо вибрану змінну в обох рівняннях. Отримані рівняння прирівнюємо та обчислюємо їх змінну.
Підставляємо цю змінну в одно з рівнянь системи. Обчислюємо другу змінну.
Приклад: Розвяжіть рівняння:
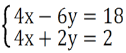
Розв'зування:
Виражаємо відносно 4x:
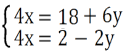
Прирівнюємо отримані рівняння та знаходимо значення
змінної y:
18 + 6y = 2 - 2y;
8y = -16;
y = -2
Підставляємо y і знаходимо значення x з другого рівняння системи:
4x = 2 - 2*(-2);
4x = 6 ;
x = 1,5
Відповідь: (1,5;4)

