приклад
Метод додавання
(віднімання)
(віднімання)

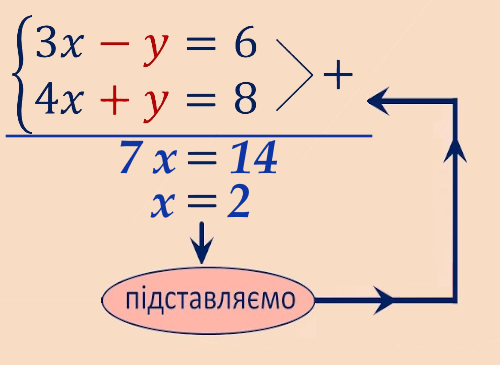
Спосіб алгебраїчного додавання (віднімання) часто використовується тоді, коли коефіцієнти при одному з невідомих чисельно рівні або їх можна звести до однакової числової величини в рівносильному рівнянні без складних обчислень.
Додаючи два рівняння здійснюємо перехід до одного рівняння з одним невідомим
Приклад: Розвяжіть рівняння:
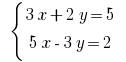
Розв'зування:
Маємо позбутись змінної y. Множимо почленно перше рівняння системи на 3, а друге – на 2
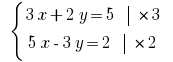
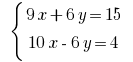
Додаємо почленно рівняння і одержуємо: 19x = 19; x = 1
Підставляємо x і знаходимо значення y з першого рівняння системи:
3*1 + 2y = 5;
2y = 2 ;
y = 1
Відповідь: (1;1)
В методі додавання можна множити не тільки на додатні числа, а і на від'ємні.
Додаючи два рівняння здійснюємо перехід до одного рівняння з одним невідомим
Приклад: Розвяжіть рівняння:
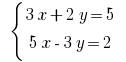
Розв'зування:
Маємо позбутись змінної y. Множимо почленно перше рівняння системи на 3, а друге – на 2
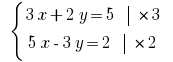
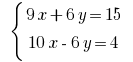
Додаємо почленно рівняння і одержуємо: 19x = 19; x = 1
Підставляємо x і знаходимо значення y з першого рівняння системи:
3*1 + 2y = 5;
2y = 2 ;
y = 1
Відповідь: (1;1)
В методі додавання можна множити не тільки на додатні числа, а і на від'ємні.

